MACAM - MACAM BANGUN RUANG
Kubus
Kubus adalah suatu bangun ruang yang dibatasi oleh enam buah sisi persegi yang kongkuren (sama dan sebangun).
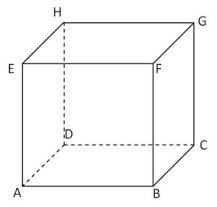
- Mempunyai 6 buah sisi yang kongkuren berbentuk persegi, yaitu ABCD, ADHE, DCHG, BCGF, ABFE, dan EFGH.
- Mempunyai 12 buah rusuk yang sama panjang, yaitu AB, BC, CD, AD, EF, FG, GH, EH, AE, BF, CG, dan DH.
- Mempunyai 8 buah titik sudut, yaitu A, B, C, D, E, F, G, dan H.
- Mempunyai 4 buah diagonal ruang, yaitu EC, HB, AG, dan DF.
- Mempunyai 12 buah diagonal bidang, yaitu AF, BE, DG, CH, AH, DE, BG, CF, AC, BD, EG, dan HF.
- Mempunyai 12 buah diagonal bidang, yaitu AF, BE, DG, CH, AH, DE, BG, CF, AC, BD, EG, dan HF.
- Pasangan sisi kubus yang berhadapan saling sejajar, sedangkan sisi kubus yang berpotongan saling tegak lurus.
Rumus-rumus pada kubus
Jika diketahui s = panjang sisi kubus, maka :
- Luas permukaan kubus (L) = 6s²
- Volume (V) = s²
- Jumlah panjang rusuk = 12s
- Panjang diagonal sisi = s√2
- Panjang diagonal ruang = s√3
Balok
Balok adalah suatu ruang yang dibatasi oleh enam daerah persegi panjang, yang terdiri atas tiga pasang yang kongkuren.
- Mempunyai 6 bidang sisi berbentuk persegi panjang, yang terdiri atas 4 pasang persegi panjang yang kongkuren, yaitu
- ABCD kongkuren dengan EFGH
- ABFE kongkuren dengan DCGH
- ADHE kongkuren dengan BCGF
- Mempunyai 3 kelompok rusuk, dimana setiap kelompok terdiri atas 4 rusuk yang sama dan sejajar, antara lain
- AB = DC = EF = HG = panjang balok (p)
- AD = EH = BC = FG = lebar balok (l)
- AE = DH = BF = CG = tinggi balok (t)
- Mempunyai 8 buat titik, yaitu A, B, C, D, E, F, G, dan H.
Rumus-rumus pada balok
- Luas balok = 2 {(p×l) + (p×t) + (l×t)}
- Volume balok = p×l×t
- Panjang diagonal balok = √p²+l²+t²
- Jumlah panjang seluruh rusuk = 4 (p+l+t)
Prisma
Prisma adalah suatu bangun ruang yang dibatasi oleh dua bidang yang sejajar dan beberapa bidang lain yang saling memotong menurut garis yang sejajar.
- Bidang alas dan bidang atas prisma dapat berupa segi banyak.
- Bidang alas dan bidang atas prisma sejajar dan kongkuren.
Rumus-rumus pada prisma
- Luas prisma = (2×luas alas) + luas selubung dengan
- Luas selubung = keliling bidang alas × rusuk tegak
- Volume prisma = luas alas × tinggi
Tabung
Tabung adalah suatu bangun ruang yang berbentuk prisma tegak yang bidang alasnya berupa lingkaran.
- Bidang alas dan bidang atas berupa lingkaran dengan jari-jari yang sama.
- Tinggi tabung adalah jarak antara titik pusat lingkaran atas dan titik pusat lingkaran alas.
Rumus-rumus pada tabung
- Luas alas = 2 π r
- Luas selimut = 2 π r t
- Luas tabung tanpa tutup = π r² + 2 π r t = π r (r + 2 t)
- Luas tabung = 2 π r² + 2 π r t = 2 π r (r + t)
- Volume tabung = π r² t
Limas
Limas adalah suatu bangun ruang dengan bidang alas berupa segi banyak dan dari bidang alas dibentuk sisi berupa yang bertemu pada satu titik.
- Pada limas segitiga, bidang sisinya berjumlah 4 buah, untuk limas segiempat, bidang sisinya berjumlah 5 buah, pada limas segi lima bidang sisinya berjumlah 6 buah, sedangkan pada limas segi enam, bidang sisinya berjumlah 7 buah.
- Limas yang bidang alasnya beraturan dan titik kaki yang garis tingginya berimpit dengan pusat bidang alas disebut limas beraturan.
- Garis tinggi sisi tegak yang ditarik dari puncak suatu limas beraturan disebut apotema.
Rumus-rumus pada limas
- Luas limas = luas alas + luas selubung limas
- Volume limas = 1/3 × luas alas × tinggi limas
Kerucut
Kerucut adalah suatu bangun ruang yang merupakan suatu limas beraturan yang bidang alasnya berbentuk lingkaran.
- Alas berbentuk lingkaran.
- Tinggi kerucut (t) adalah jarak antara puncak kerucut dengan titik pusat lingkaran alas kerucut.
- Panjang garis pelukis (s) = TA = TB.
- AB adalah diameter lingkaran alas kerucut.
Rumus-rumus pada kerucut
- Luas alas = π r²
- Luas selimut = π r s
- Luas kerucut = π r (r + s)
- Volume kerucut = 1/3 × luas alas × tinggi = 1/3 π r² t
Bola
Bola adalah suatu bangun ruang yang terjadi jika setengah lingkaran diputas mengelilingi diameternya.
Rumus-rumus pada bola
- Luas bola = 4 π r²
- Volume bola = 4/3 π r²











Tidak ada komentar:
Posting Komentar